warehouse/content/physics/Forces.md

title, date

title	date
Forces	2024-09-07

One must always start a study into the heavily crippled IB editions of the glorious subject of Physics with the initial understanding that the road ahead leads to pain immeasurable.

-> Prime of the Faith

Track of Variables

Important

YOU WILL NEED TO KNOW WHAT VECTORS ARE MATHEMATICALLY. THEY WERE ON THE LAST TEST, EVEN MORE SO NOW.

• \vec{a} is the acceleration vector of an object. Has a frame of reference.
• \vec{F} is a force vector. Has a reference frame.
• sum{\vec{F}} is the sum of all force vectors acting on an object. Also has a reference frame.
• m is mass, a scalar quantity

Newton's laws of Motion

Force

• force is any kind of push or pull on an object.
• the force applied on an object due to gravity is called the force of gravity
• Any object requires force to get moving from rest
• In order to alter the magnitude or direction of movement, you again are required to apply force
• mass \ne weight
• Force is a vector :)
• mass isn't exactly what you think it is, check here.
• the gram and its deviates are representative of mass not weight.

Newton's First Law of Motion

The textbook has a surplus amount of blabber here, so I think i will spare you of it for now.

Every object continues in its state of rest, or of uniform velocity in a straight line, as no net force acts on it.

Essentially, the same velocity vector remains without any acceleration acting on it.

Also important to note is that Newton's first law does not hold true in every reference frame. If your reference frame is fixed in an accelerating car, or any accelerating object with force acting on it in order to accelerate the velocity in any way, other objects may be moved toward you. For example, a cup on the dashboard of said car. As long as the cup was in rest in relation to the car when it was in rest or with a constant velocity, the cup might accelerate toward you, while you perceive that no force had acted on the cup in order that it may behave this way. Such reference frames have since been labeled as inertial reference frames. Reference frames that aren't accelerating in this manner are therefore called non-inertial reference frames. You can also decide between the two based on if the \mathrm{1}^st law of motion hold true.

Newton's Second Law of Motion

The second law makes use of the concept of mass, so that seems to be next on the agenda.

Mass

You might have previously heard the Newtonian definition of mass, which makes it synonymous with a measure for the "quantity of matter" in an object. However, physicists have since come to a consensus that this is a definition sans precision. Mass is the *measure of the inertia of an object.^ The more mass an object has, the greater the force needed to give it a particular acceleration. In other words, get it moving.

The Law

The acceleration of an object is directly proportional to the net force acting on it, and is inversely proportional to its mass. The direction of the acceleration is the direction of the net force acting on the object.

This can directly be written into math like so:

\vec{a}=\frac{\sum{\vec{F}}}{m}

Or as the more commonly seen:

\sum{\vec{F}}=m\vec{a}

Or in an even simpler manner if you assume a 1D world: F=ma. No matter the form, all it means is that the net force on the object (as show in the summation of force vectors), divided by the mass, is the acceleration applied to the object. Note first that you will almost neevr deal with this equation is the hyper-simple singular dimensional world, because most problems require gravity to be considered. Another valuable insight is how gravity is not a part of this equation, as it a phenomenon that creates a force of its own. These forces can also be broken down along side the acceleration vectors into their own dimensions. Read about vectors in Vectors and Kinematics if you don't understand the following.

\sum{F_x}=ma_x

\sum{F_y}=ma_y

\sum{F_z}=ma_z

\sum{F_\dots}=ma_\dots

And so on.

Newton's Third Law of Motion

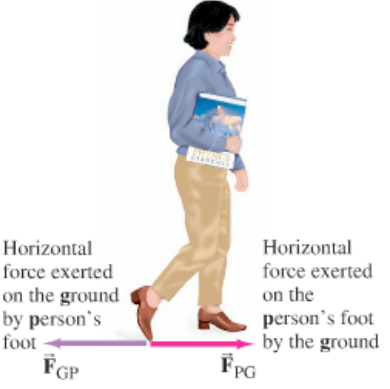
Whenever one object exerts a force on a second object, the second exerts an equal force in the opposite direction the first.

This is mathematically put down as \vec{F}_1=-\vec{F}_2. Below, \vec{F}_{GP}=-\vec{F}_{PG}.

#physics