tension 2

content/physics/Forces.md

@@ -121,6 +121,18 @@ Until this point, we've been ignoring the mysterious forces that enact the force
 
 ![](https://digestiblenotes.com/images/physics/alevel/tug1.png)
 
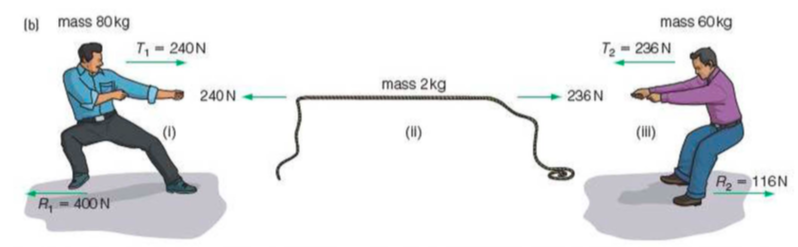
-As shown in the image, tension on a string or another mass-less is a result of Newton's $3^{\mathrm{rd}}$ law of motion. The men pull on the rope, exerting the two middle forces labeled $240$ N and $236$ N respectively. As a result, the rope pulls the blue shirted man by 240 N. In order to accelerate the whole system to left by $2 \mathrm{m}/\mathrm{s}^2$, Alan has to exert $400$ N of force pushing the earth to the right. As a *result* of Newton's $2^\mathrm{nd}$ law of motion, the Earth exerts 400 N of force on the blue shirted man, leftwards. This is labeled $R_1$. 
+As shown in the image, tension on a string or another mass-less is a result of Newton's $3^{\mathrm{rd}}$ law of motion. The men pull on the rope, exerting the two middle forces labeled $240$ N and $236$ N respectively. As a result, the rope pulls the blue shirted man by $240$ N. In order to accelerate the whole system to left by $2 \mathrm{m}/\mathrm{s}^2$, Alan has to exert $400$ N of force pushing the earth to the right. As a *result* of Newton's $2^\mathrm{nd}$ law of motion, the Earth exerts 400 N of force on the blue shirted man, leftwards. This is labeled $R_1$. 
+
+To actually calculate the tension on the rope, you have a couple variables to consider: $\vec{F_T}=\langle T\sin\theta, T\cos\theta\rangle$, and $T=||\vec{F_T}||$. The tension amounted to $4$ N because $\theta=0$, $\therefore \sin\theta=0$. And the magnitude of the tension vector itself is:
+$$
+\sum{\vec{F_r}}
+$$
+Or the sum of all forces being exerted, on the rope. In situations like elevator cable problems, $\theta=\frac{\pi}{2} \therefore \cos\theta=0$[^1]. If the elevator is accelerating upward at $a \mathrm{m}/{s}^2$, then[^1] 
+
+$$
+\sum{\vec{F}}=\langle ma+mg;-\tfrac{\pi}{2}\rangle
+$$
+
+[^1]: I'm working in radians here.
 
 #physics